Why masses attract
Scenario 1
This was my first explanation, from Feb 2015, although I had been thinking about the idea for many years before that.Relative acceleration
In my Mass and Charge article I introduce the concepts of:
A force induced by relative acceleration.
Presence.
For an explanation of unfamiliar terms and concepts in this article, please first read my 'Mass and Charge' article, at least up to Conjecture 6.
If the
attraction between stationary masses is to be explained by a force
induced by relative acceleration, then from the point of view of one
mass, the other will have to appear to accelerate away. In other
words each mass will have to be subject to the accelerating presence
of the other. I now have to explain the origin of this proposed
acceleration.
Curved
space-time around a massive particle
"Matter tells
space how to curve, and space tells matter how to move." -
attributed to John Wheeler - from Wikipedia.
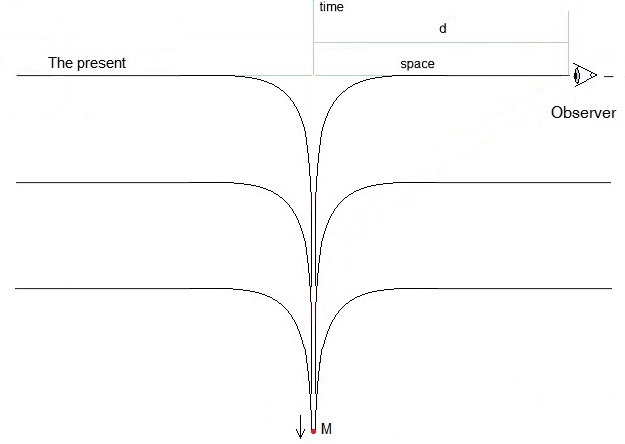
This is a space-time diagram with one space and one time co-ordinate.
A massive particle M causes space around it to curve into a tube-like structure, a well. In this scenario, M (represented by a red dot in the diagram) causes space to be deformed in the time direction. The curved black lines represent space at different times.
Space at the 'present time', is assumed to progress in an upward direction at a constant rate. Another way of looking at it is that the observer can be considered stationary and M recedes into the past at constant rate.
Space far from M is flat. Here time progresses at a constant rate. I call the shape of this region 'plane-like'. Space close to M is curved. I call the shape of this region 'tube-like'. What might be considered to be the 'surface' of the particle is the point (the surface in three space dimensions) of maximum curvature, between the plane-like region and the tube-like region.
If it were possible to be an observer in the tube-like region, M would appear to move away at an almost constant rate. How can M appear to accelerate away from an observer in the plane-like region? The acceleration has to be proportional to 1/d2. The distance d is the distance from the observer to the centre of M in flat space.
An
analogy
Imagine a very large air-filled space. A
pipe leading outside the space has its mouth at the centre of the
space. A piston in the pipe draws air from the space. The piston
moves at a constant rate. Air is drawn from the space at a constant
rate. Just inside the mouth of the pipe, air moves at a constant
rate. In the surrounding space air is drawn towards the mouth of the
pipe. The air accelerates towards the mouth of the pipe. This
acceleration is greatest near the mouth of the pipe. Further away,
the acceleration is less as the air passes through spherical surfaces
of greater and greater area.
I chose air in the analogy because, if you do the maths, you find that the acceleration of an incompressible liquid does not vary with 1/d2.
The conclusion I draw from the analogy is that an observer in the plane-like region is subject to the accelerating presence of M, as if M were accelerating away from him. It's the geometry of space-time around M that makes M appear to accelerate.
The
implications of this scenario
This scenario
shows how the concept of a force induced by relative acceleration
might be used to explain the attraction between stationary masses in
the plane-like region. Things get more interesting in the curved
space-time region.
Near
to the a massive body, the 1/d2
force relationship no longer holds. There is a region of maximum
acceleration around M between the tube-like and plane-like regions.
Closer still, the attractive force becomes increasingly weaker than
the 1/d2
value. A test particle in the tube-like region will experience almost
no acceleration towards M, and will be trapped as the attraction
towards M increases with distance from M as far as the region of
maximum acceleration.
Black
Holes
If the Event Horizon of a Black Hole
is the surface of maximum curvature, then the region within it is
tube-like and the attractive force decreases almost to zero near the
mass at the centre. The so-called 'spaghettification' will not
continue all the way to the centre, maybe not much past the event
horizon.
This scenario is unsatisfactory because if the presence of M has to keep a constant angle (the speed of light) to the local space dimension, at every instant, then in the tube-like region presence and radiation is always directed back towards the centre of the well and cannot escape.
On the other hand, if this angle becomes more acute close to M, and approaches zero degrees where space-time is most distorted (in the tube-like region), then the path of light might closely follow the local space dimension past the surface of maximum curvature and on to an observer.

This would explain why the gravitational presence of a Black Hole is experienced outside the Event Horizon. It also offers the possibility that radiation might escape from a Black Hole, though whether a singularity can generate radiation is debatable.
Scenario 2
I
started thinking about this scenario after deriving an equation for
the additional force
between passing masses, in
my 'Mass and Charge' article, in
the summer of 2015. This scenario does not require space-time to be
curved.
The force between stationary masses is:
f
= Kg.m1.m2/d2 (where Kg
= G, the gravitational
force constant)
In
my 'Mass and charge' article I discuss the concept of a force
induced by relative acceleration. Later
in the article I derive an equation for the
additional force between passing masses.
f
= Kg.m1.m2.v2.(sin2θ)/c2.d2
θ is defined in
the same article in 'Preface to the motor effect'. There I show that
passing objects actually accelerate relative to one another.
This
force is induced by the relative acceleration between the masses.
At
closest approach,
f
= Kg.m1.m2.v2/c2.d2 (sinθ
= π, sin2θ
= 1)
When v =
c,
f
= Kg.m1.m2/d2
So, the
force between stationary masses is equal to the additional force that
would exist between masses passing at the speed of light.
The
scenario is shown in the following diagram.
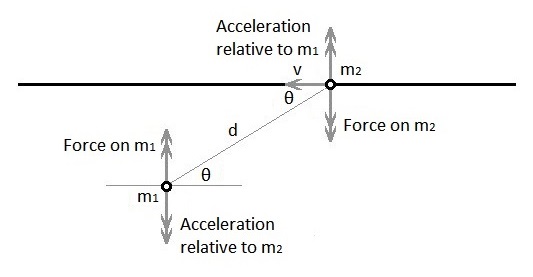
m1 is considered to be stationary and m2.is passing m1 at a constant velocity v.
I have seen it proposed in many articles that the present time moves forward at a velocity c. I'm not sure exactly what that means or even of it makes sense. However I'm going to use that proposal to investigate the relationship between an observer and the observed object.
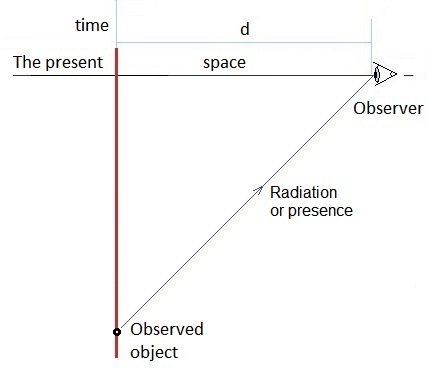
In this space-time diagram the observer is considered to move forward, in time, at velocity c. The observed object, the red vertical line, exists 'all the time' and can be considered stationary in space-time. The observer only sees one instant, at a time, in the existence of the object. From the observer's point of view, the object is moving into the past at velocity c.
The object is passing the observer at a constant velocity, c, in space-time.
If the explanation for objects passing in space is also valid in space-time this could explain the force between stationary masses.
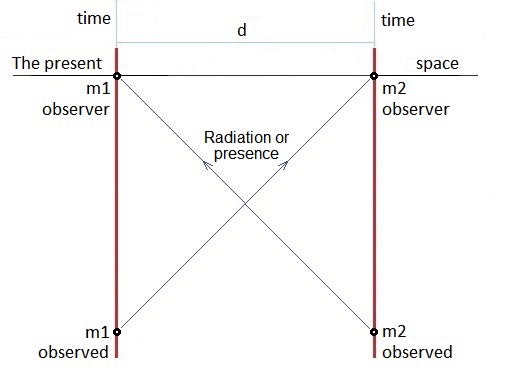
The observer and the observed object
There is a problem here with the dual role of the masses. How can a mass act as an observer moving forwards in time and also act as the observed, a stationary object, extended in the time dimension? As yet, I have no explanation for this.
Mike Holden – Oct 2016 to Apr 2017