Mass and charge
In this article I describe a new way of explaining the interactions between masses and between charges. I find that I can explain all the common phenomena.
This approach has revealed some other interesting insights, including:
- A new explanation of Radiation Resistance.
- A new phenomenon, the additional force between passing masses, equivalent to the additional force between passing charges.
- An
explanation of the stability of the orbits of objects in a disc around
a rotating massive object, based on a phenomenon akin to inertial frame
dragging.
Mass and Inertia
My first memorable experience of inertia occurred when I was about 10 years old. I grew up in a village in the Midlands in the 1940s and 50s. In those days houses were heated by coal and every week a train delivered three or four coal trucks to a siding at the village station and took away the empties. The siding was not fenced and as boys we often went there to watch the coal-men or to just play. Most of the time the siding was unattended.One day, we noticed that one of the empty coal trucks was uncoupled from the others and the brake was off. Like most boys of our age we couldn't see any danger and decided to try and push this truck to see if we could get it moving. After much heaving we managed to start it, if only very slowly. We were used to playing with Dinky cars that you pushed along the floor and they stopped after a few feet. This thing had a large mass and very little rolling resistance and it just kept on rolling.
We realised that if it didn't stop it would hit the buffers about thirty yards away. We thought it might do some damage so, being silly we ran round to the front and tried to push it to a standstill. To my surprise it was as difficult to stop as it was to start - inertia in action. It's much easier to push something away from you than to try to push something that is coming towards you and it took a lot of effort, together with the danger that we might get run over, but eventually we managed to bring it to a stop.
The experience frightened us so much that we ran home and never played on the siding again.
In the 1970's I entered a creative period of my life that has lasted, on and off, until the present day. It was then that I started thinking about mass and inertia and came up with an idea that later I developed to include electricity as well.
A force induced by relative acceleration
Imagine an astronaut in his accelerating space ship far from any planet or star. He experiences a force pushing him back into his seat. What causes this force?
From the astronaut's point of view he could be stationary and the rest of the universe could be accelerating past him in the same direction as the force. Could this relative acceleration be the origin of the force? The universe is a very large mass at a very large average distance. Could a much smaller mass at a much smaller distance have a similar effect?
I think I can show that the answer is 'Yes'. If this is so, the force will depend on the masses, their relative acceleration, their distance apart and the properties of the intervening space.
I call this effect the principle of a force induced by relative acceleration.
It seems that an accelerating mass causes a force to act on another mass in the same direction.
Next, I need to introduce one more concept.
Gravitational Presence
Events happening a light year away take one year to affect us, and it is 100 years before we become aware of an event occurring 100 light years away. So an object or event elsewhere in the universe cannot affect us instantaneously. What can affect us is the 'field strength' of the object or event at our point in space and time. I call this field strength 'Presence'. Presence can be universal or local, static or dynamic and, as it turns out, gravitational or electrical.
Mass comes in only one variety. Masses attract one another. This attraction is known as gravity. The presence of a point or spherical massive body varies with the inverse of the square of its distance (in flat space-time). The effect of masses is cumulative. This is why mass has universal presence.
The presence of a linear body varies with the inverse of its distance, when this distance is small compared with its length.
The presence of a planar body does not vary with distance, when this distance is small compared with its dimensions.
Universal presence is the presence of the whole visible universe.
So when the astronaut experiences a force when accelerating, he is accelerating with respect to the gravitational presence of the rest of the universe at his point in space and time.
Note:
There is no difference, in principle, between local and universal presence. However, it is sometimes convenient to deal with them separately.
Electric charge
In my youth I trained as an electrical engineer but was never entirely happy with Faraday's concept of magnetic flux, lines of force etc. while appreciating the help this gives in visualising what goes on and the aid to calculation it provides. I was interested in finding a deeper understanding.Historically, electricity and magnetism developed as two separate subjects and were only combined in the 19th century by the work of Faraday, Maxwell and others. Charge is the basic phenomenon. All electrical and magnetic effects can be described in terms of charge. Magnetism is the result of moving charges.
In this section I will attempt to explain electrical interactions using the principle of a force induced by relative acceleration. There will be no mention of 'lines of force', 'flux' or magnetism.
Electrical Presence
Charge comes in two varieties, positive and negative. Positive charges repel one other, and negative charges repel one other too, but a positive charge and a negative charge attract one other. The presence of a point or spherical charged body varies with the inverse of the square of its distance.
It is assumed that the universe has an equal number of positive and negative charges. Because opposite charges attract they tend to stay together. The presence of one is cancelled out by the opposite presence of the other. The outcome of this is that although electric charge appears to be vastly more powerful than mass, its presence over cosmic distances is effectively zero.
So, electric charge has no universal presence. This is why electrons and protons (having very small masses but relatively large charges) can be accelerated to relativistic speeds.
Electrons
In one sense an electron can be considered to be a point particle with a very small mass and one unit of negative charge. Electrons are the negative components of atoms. In atoms they surround the positive nucleus in 'shells'. Each shell consists of electrons up to a maximum number, at a specific 'energy level', depending on the number of protons in the nucleus. The charge on an electron has the same value as the charge on a proton but is opposite in sign. The outer electrons that are furthest from the nucleus are less tightly bound to the atom than the inner ones. In bulk metals some of these outer electrons are free to move away from an individual atom and are effectively shared. Given the right circumstances these free electrons can constitute an electric current.
Unfortunately, for historic reasons, what engineers call an electric current is considered to move in the opposite direction to the flow of electrons.
Electrical Resistance
If an electric field (also called a voltage, an emf or potential difference) is applied across the ends of a conductor, for example a metallic wire, the free electrons in the wire will be attracted towards the positive end and repelled by the negative end. If the conductor is part of an electrical circuit, electrons will flow along the wire and round the circuit.
Electrons, in a vacuum, accelerate in an electric field. However, the electron flow in a wire stabilises at a particular level. This level is proportional to the applied voltage. This means that if you double the voltage you double the flow. The cause of this stabilisation is called electrical resistance and it results in heat being generated in the wire rather than the electrons being accelerated beyond a particular velocity. Energy is transferred from moving electrons to atoms in the wire when they collide.
If an alternating voltage is applied to a circuit in which resistance dominates, this stabilisation results in the current being 'in phase' with the applied voltage. Without resistance the current would be much greater and would lag the voltage by 90 degrees.
Self-inductance
Another effect that limits the current in a conductor, at least initially, is called self-inductance. Self-inductance slows down the rate at which the current reaches the level determined by resistance.
Because the free electrons came from neutral atoms in the wire, the atoms each have an excess positive charge (protons). Only the free electrons are able to move. When a potential difference is applied across the ends of the conductor, these electrons initially accelerate relative to the electrical presence of the excess protons which surround them and experience a force opposing their motion. This is equivalent to inertia, when a mass is accelerating relative to universal gravitational presence. As the electron flow stabilises, this force decreases.
It seems that an accelerating charge causes a force to act on another unlike charge in the same direction.
If an alternating voltage is applied to a circuit in which self-inductance dominates, this effect results in the current lagging the applied voltage by 90 degrees.
This phenomenon could be an explanation for Radiation Resistance.
Mutual inductance (the transformer effect)
Mutual inductance is the property of a conductor by which a change in current in the conductor induces a voltage in a nearby conductor. - from Wikipedia. |
This is a very simple transformer - no coils, no iron - just two parallel conductors. An alternator is connected to the primary conductor. I have included a resistor in each circuit to limit the currents. For simplicity, the conductors are assumed to have zero resistance. Only the free electrons are able to move.
In the primary conductor, the free electrons move left and right with simple harmonic motion (sine wave motion). Consider the situation when they are at the right hand limit of travel. They have maximum acceleration to the left and their velocity is zero.
The free electrons in the secondary conductor experience maximum force at this time. In a real transformer, with a resistive load, the secondary current is out of phase with the primary current (ignoring phase shifts due to losses). So, the free electrons in the secondary conductor are accelerating to the right. This means that the force is acting from left to right.
The reverse happens when the primary electrons are at the left hand limit of travel and have maximum acceleration to the right.
It seems that an accelerating charge causes a force to act on another like charge in the opposite direction.
In addition, the accelerating electrons in the secondary conductor cause the electrons in the primary conductor to experience a force in the same sense as their acceleration. This positive feedback results in the primary and secondary currents increasing to a level limited by the resistance of the two circuits. This is observed in a real transformer. The primary current increases when a lower value resistor is connected to the secondary circuit.
One quarter cycle after the time of maximum acceleration, the currents in the two conductors are at a maximum in opposite directions. This causes the conductors to repel each other twice per cycle (due to the Motor effect, explained later). This repulsion could be the explanation for Radiation Pressure.
Progress so far
Conjectures 1 - 3- Accelerating one mass can cause another mass to experience a force in the SAME direction.
- Accelerating one charge can cause an UNLIKE charge to experience a force in the SAME direction.
- Accelerating one charge can cause another LIKE charge to experience a force in the OPPOSITE direction.
Conjectures 4 - 5
Bodies that normally attract:
- Accelerating one such body can cause another such body to experience a force in the SAME direction.
- Accelerating one such body can cause another such body to experience a force in the OPPOSITE direction.
Radiation
A radio transmitter aerial and a radio receiver aerial is essentially the same scenario as the transformer described above. Energy is transferred from one to the other by the same process, only in the case of radio the distances are far greater. Radio is just the low frequency version of light and other electrical (electro-magnetic) radiation.Let's consider other radiation scenarios.
| Consider a positive charge and a negative charge made to accelerate away from one another, by an explosion for instance. How will this charge separation affect a positive or a negative charge some distance away? ('q' is the symbol for charge). | 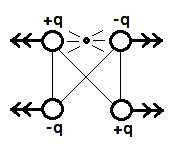 |
The positive charge accelerating to the left will cause the second positive charge to experience a force to the right and the second negative charge to experience a force to the left. The negative charge accelerating to the right will cause the second positive charge to experience a force to the right and the second negative charge to experience a force to the left. The effects on each charge are additive and the charges accelerate. Radiation transfers energy from the first pair of charges to the second pair.
| Consider two masses made to accelerate away from one another, by an explosion for instance. How will this mass separation affect a third mass some distance away? | 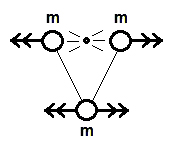 |
The mass accelerating to the left will cause the third mass to experience a force to the left. The mass accelerating to the right will cause the third mass to experience a force to the right. The effects on the third mass are subtractive. No radiation takes place. (Even if the accelerating masses are different, their 'mass x acceleration' is the same)
Conjecture 6
- On
a cosmic scale and to a first approximation, charge exhibits radiation
but no presence, and mass exhibits presence but no radiation.
Local effects
This may be true on a cosmic scale but on a local scale things are different. Here are two examples:- The good old pith ball experiment. Two pith balls, both positively (or negatively) charged, suspended by insulating threads, repel one another. Local electrical presence in action.
- Depending on how you define radiation... If radiation is the transfer of energy across empty space from one body to another, then the earth-moon system demonstrates gravitational radiation (gravitational waves). Tidal effects transfer energy from the earth to the moon, increasing the moon's orbital energy at the expense of the earth's rotational energy.
Radiation Resistance
Radiation resistance is that part of an antenna's feedpoint resistance that is caused by the radiation of electromagnetic waves from the antenna, as opposed to loss resistance (also called ohmic resistance) which generally causes the antenna to heat up. - from Wikipedia.Radiation Resistance is not electrical resistance in the normal sense but the 'resistance to acceleration' of free electrons in a transmitter aerial. It appears as soon as current starts to change. This indicates that it is a local effect within the aerial itself. It cannot be caused by interaction with the receiving aerials (as proposed in the Wheeler-Feynman Absorber theory) for two reasons. Any such interaction would have to be immediate and coherent. However, there will be a time delay in any feedback from a receiver aerial due to the distance between the transmitter and receiver aerials. Also, these feedback signals will be out of phase with one another and not coherent when arriving at the transmitter due to the different distances between the transmitter and various receivers.
I propose that Radiation Resistance is due to Self-inductance in the transmitter aerial. When the free electrons accelerate, relative to the electrical presence of the excess protons which surround them, they experience a force opposing their motion as described in the Self-inductance topic.
If this is so, electrons made to accelerate in a vacuum, well away from any excess protons, will not experience Radiation Resistance as there is no Universal electrical presence.
It is interesting to note that in J J Thompson's 1897 experiment, to determine the ratio of charge to mass for an electron, Radiation Resistance is not taken into account. Only the effect of the mass of the electron, as it accelerates towards the centre of curvature of its path, is used in the calculation. This makes sense if there is no Universal electrical presence.
More phenomena
With one more requirement, which I will explain in 'Preface to the motor effect', the following effects can be explained by the principle of a force induced by relative acceleration.Charge
- The motor effect - The force between two parallel current-carrying conductors when the currents are in the same, or the opposite, direction.
- The generator effect - The force on electrons in a conductor when in the presence of a moving, current-carrying conductor.
- The different properties of beams of electrons and electrons moving in wires.
- The force between passing charges.
- The force between static charges.
- The motion of an electron, in a vacuum, passing across a pole of a magnet.
- Why charges attract or repel..
- Inertial frame dragging.
- Perihelion precession.
- The force between passing masses.
- The force between static masses.
- Inertia and the mass of the Visible Universe.
- Negative mass..
- Why masses attract.
Conventional
Terminology
In the following topics I refer to conventional terminology. Here is a brief description of the physical units and the conventional explanation of the relevant electrical effects.
The International System
of units
(SI units)
Four
of the fundamental SI units are the Metre (distance), the Kilogram
(mass), the Second (time), and the Ampere (electric current).
The Ampere is defined as that current which when passing through each of two parallel long thin conductors one metre apart, in a vacuum, results in a force between the conductors of 2 x 10-7 Newtons, per metre length.
In SI units the unit of charge, the Coulomb, is defined as one 'Ampere x Second'.
The
force between conductors
In conventional terminology the force between two parallel
current-carrying conductors in a vacuum is expressed as:
f
= (μ0/2π).i1.i2.l/d
-
μ0 is the 'magnetic constant', known earlier as the 'magnetic permeability' of a vacuum.
- i1 and i2 are the currents in the conductors.
- l is the length of each conductor.
- d is the distance between the conductors.
μ0, has a value of 4π x 10-7 = 1.2566 x 10-6 in SI units.
The value of
μ0
can be derived from the definition of
the Ampere. See the
definition of the Ampere and the force equation above.
μ0
=
f.2π.d/(i2.l) = (2 x 10-7).2π.1/(1.1) = 4π
x 10-7
μ0/4π
is known as the magnetic force
constant, Ka, so:
The
force between charges
In conventional terminology the
force between two static
charges in a vacuum is expressed
as
f
= (1/4π.ε0).q1.q2/d2
-
ε0 is the 'electrostatic constant', known earlier as the 'electric permittivity' of a vacuum.
- q1 and q2 are the charges.
- d is the distance between the charges.
f = Ke.q1.q2/d2
ε0 was found by experiment to have a value of just under 8.8452 x 10-12 in SI units. It is now defined by the following equation:
ε0 = 1/(μ0.c2)
Where c is the speed of light in a vacuum, 2.9979 x 108 in SI units.
Ke/Ka = (1/4π.ε0)/(μ0/4π) = 1/(μ0.ε0)
So:
Ke/Ka = 1/(μ0.ε0) = c2
Preface to the motor effect
Consider two parallel conductors. A current flows in each conductor. If the currents are in the same direction, the conductors attract one another. If the currents are in opposite directions, the conductors repel one another.If this is to be explained by the principle of a force induced by relative acceleration, there must be relative acceleration between the charged particles in the two conductors.
Objects passing
Over the years I have shown this scenario to several mathematicians. They all said that there was no relative acceleration between the objects. This has delayed me writing this article for over 30 years. However, I keep coming back to it as their relative velocity is certainly not constant.
Also, the Doppler Effect suggests an acceleration in this scenario. A stationary observer hears a falling pitch from the horn of a passing car. A falling pitch indicates a relative acceleration away from the observer.
Calculating the relative acceleration
Consider a stationary object, A. A second object, B, travelling in a straight line at velocity v, passes A.
What is the relative acceleration of B with respect to A?
How does B appear to accelerate from the point of view of A?
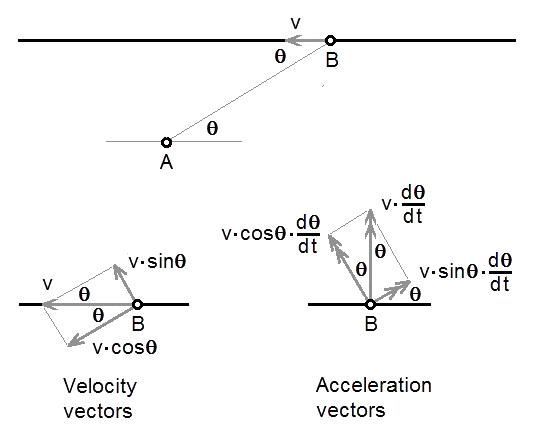 |
The component of v along the line joining A to B is v.cosθ.
The component of v at right angles to the line joining A to B is v.sinθ.
The first differential of v.cosθ with respect to θ is is -v.sinθ, (negative means it is in the opposite direction).
The first differential of v.cosθ with respect to time (acceleration) is is -v.sinθ.dθ/dt.
Similarly, the first differential of v.sinθ with respect to time (acceleration) is is v.cosθ.dθ/dt.
The vector sum of these two is: (v.sinθ.dθ/dt).sinθ + (v.cosθ.dθ/dt).cosθ = v.dθ/dt in the direction shown.
The acceleration of Object B relative to Object A is v.dθ/dt at right angles to B's direction of travel and AWAY from A.
The direction of v.dθ/dt is at right angles to Object B's direction of travel because:
- The velocity of Object B, v, is constant. (no acceleration)
- The sum of the components of the acceleration vectors in the direction of travel is: (v.cosθ.dθ/dt).sinθ - (v.sinθ.dθ/dt).cosθ = 0
The scenario is the same as above.
C is the point of closest approach.
The distance from C to A is d.
The distance from C to B is l.
The distance from A to B is d/sinθ.
Consider a small time duration, δt.
Object B moves a distance δl , while moving through an angle δθ about A.
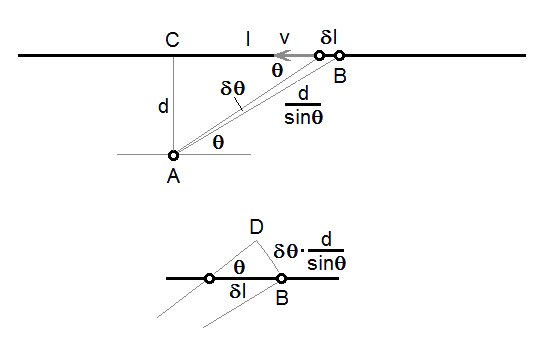 |
As δt tends to 0, δθ.d/sinθ and δl.sinθ tend to become equal.
δθ.d/sinθ = δl.sinθ
δθ = δl.(sin2θ)/d
δθ/δt = (δl/δt).(sin2θ)/d
In the limit when δt = 0,
δθ/δt = dθ/dt and δl/δt = dl/dt
So,
dθ/dt = (dl/dt).(sin2θ)/d
But dl/dt = v. So,
dθ/dt = v.(sin2θ)/d
Finishing the calculation
Going back to:
The acceleration of Object B relative to Object A is v.dθ/dt at right angles to B's direction of travel and AWAY from A.
Now,
v.dθ/dt = v2.(sin2θ)/d
So, the acceleration of Object B relative to Object A is v2.(sin2θ)/d at right angles to B's direction of travel and AWAY from A.
When Object B is at C (at closest approach)
θ = π/2
and sinθ = 1
So,
v2.(sin2θ)/d
= v2/d
The motor effect
The forces described here are in addition to
the static electrical forces on the particles.
Consider two parallel conductors, A and B, in a vacuum. The same
current is flowing in each conductor. Because the conductors are
electrically neutral, only the free electrons and the excess protons
take part in the interactions.
Currents in the same
direction
The free electrons in each conductor are moving in same direction. They
are passing the excess protons in the other conductor with a velocity
v. There is no relative velocity between the free electrons on one
conductor and the free electrons in the other conductor.
Let's look at the relative accelerations and forces on the free
electrons and the excess protons in the conductors.
-
The relative acceleration between a free electron in Conductor A and an excess proton in Conductor B is proportional to v2/d at right angles to the conductors and away from one another.
-
The relative acceleration between a free electron in Conductor A and all the excess protons in Conductor B is proportional to v2/d at right angles to the conductors and away from one another.
-
The relative acceleration between all the free electrons in Conductor A and all the excess protons Conductor B is proportional to v2/d at right angles to the conductors and away from one another.
-
So, the force between all the free electrons in Conductor A and all the excess protons in Conductor B is proportional to v2/d (= k.v2/d) at right angles to the conductors and towards one another. (Conjecture 3)
Similarly:
-
The force between all the free electrons in Conductor B and all the excess protons in Conductor A is proportional to v2/d (= k.v2/d) at right angles to the conductors and towards one another.
As the free electrons in each conductor are moving in same direction, there is no relative velocity between them, no relative acceleration and therefore no additional force between them.
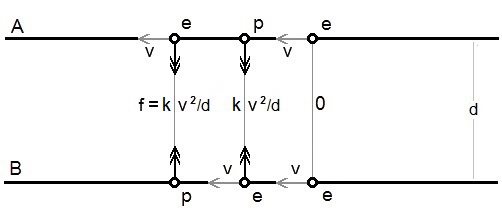 |
So the total force on the conductors is k.v2/d
+ k.v2/d
= 2k.v2/d
and they attract one another.
Currents in opposite directions
The free electrons in each conductor are moving in opposite directions.
They are passing the excess protons in the other conductor with a
velocity v, and are passing the free electrons in the other conductor
with a combined velocity of 2v.
-
The force between all the free electrons in Conductor A and all the excess protons in Conductor B is k.v2/d at right angles to the conductors and towards one another.
-
The force between all the free electrons in Conductor B and all the excess protons in Conductor A is k.v2/d at right angles to the conductors and towards one another
-
The force between all the free electrons in Conductor A and all the free electrons in Conductor B is k(2v)2/d = 4k.v2/d at right angles to the conductors and away from one another. (Conjecture 2)
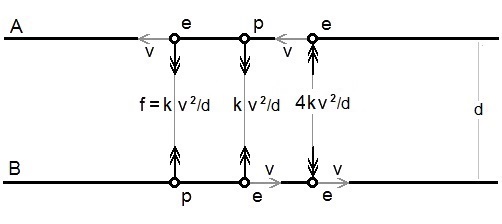 |
So the total force on the conductors
is k.v2/d
+ k.v2/d
- 4k.v2/d
= -2k.v2/d
and they repel one another.
The value of k
Call the charge on an electron, or proton, -q or +q.
Besides v2/d,
the force between the conductors depends on several factors which are
bound up in k.
- The electrical property of the intervening vacuum. (Call it Pe)
- The length of the conductors (Call it l)
- The free electron (or excess proton) charge per unit length in Conductor A. (Call it dq/dl)
- The free electron (or excess proton) charge per unit length in Conductor B. (Call it dq/dl)
- The inverse of the distance between the conductors. (Call it 1/d) - Linear bodies.
Combining the above factors into k.
k = Pe.(dq/dl).(dq/dl).l/d
k
= Pe.(dq/dl)2.l/d
The force between the conductors:
f = 2kv2/d
f = 2Pe.(v2/d).(dq/dl)2.l/d
But, v = dl/dt:
f
= 2Pe.(dl/dt)2.(dq/dl)2.l/d2
f = 2Pe.(dq/dt)2.l/d2
But,
dq/dt = current, i:
f
= 2Pe.i2.l/d2
For
different electron flows, v1 and
v2,
in the same direction:
f = k[(v1)2
+ (v2)2
- (v1
- v2)2]/d2
f = 2k.v1.v2/d2
f =
2Pe.i1.i2.l/d2
(attraction)
For different electron flows, v1 and v2, in opposite directions:
f = k[(v1)2 + (v2)2 - (v1 + v2)2]/d2
f = - 2k.v1.v2/d2
f = - 2Pe.i1.i2.l/d2 (repulsion)
Compatibility
with conventional terminology
In conventional terminology the force between two conductors (different
currents) in a vacuum is expressed as:
f = (μ0/2π).i1.i2.l/d or f = 2Ka.i1.i2.l/d
So, the magnetic force constant Ka = Pe/d
But:
Ka = Ke/c2
So:
f = 2Ke.(1/c2).i1.i2.l/d
The force between the conductors:
f = 2Pe.i1.i2.l/d2 = 2Ka.i1.i2.l/d = 2Ke.i1.i2.l/c2.d
I have described the motor effect in great detail and it seems I have established the principle. I am now going to describe the remaining phenomena in somewhat less detail.
The generator effect
The forces described here are in addition to the static electrical forces on the particles.There are two parallel conductors, A and B. Conductor A has a constant current flowing along it and it is moving towards Conductor B at a constant velocity.
- vc is the velocity of Conductor A towards Conductor B.
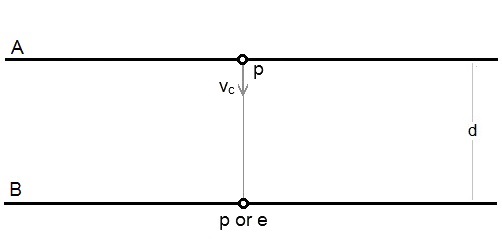 |
Because the particles are travelling directly towards one another at a constant velocity, there is no relative acceleration and no additional force between them.
Now consider a typical free electron somewhere near the centre of Conductor A, and its effect on another free electron or excess proton opposite it in Conductor B.
- ve is the velocity of the free electron along Conductor A.
- vr is the resultant velocity of the free electron in Conductor A.
- The angle between ve and vr is θ.
- fp is the force between the free electron in Conductor A and the excess proton in Conductor B .
- fe is the force between the free electron in Conductor A and the free electron in Conductor B .
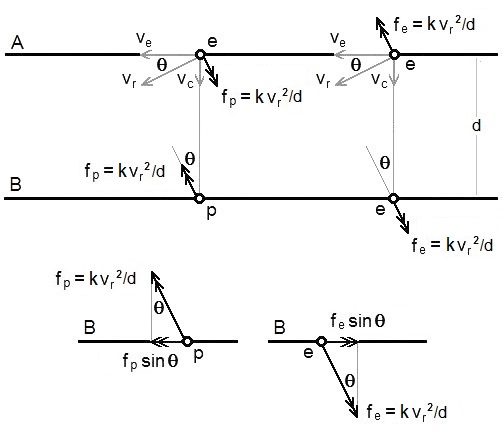 |
- There is a force fp.sinθ on the excess proton in Conductor B in the same direction as the electron flow in Conductor A.
- There is a force fe.sinθ on the free electron in Conductor B in the opposite direction to the electron flow in Conductor A.
- The forces perpendicular to the conductor cancel out until the current begins to flow in Conductor B. Then, as in the case of the motor effect, the conductors repel.
- As
in the transformer scenario, there is a positive feedback effect
causing the current in Conductor A to increase as the current increases
in Conductor B.
The different properties of electron beams and electric currents in wires
Although we think of electron beams as being electric currents, their behaviour is quite different from electric currents in wires. Here are some of the differences.| Electron beam(s) | Electric current(s) in wire(s) |
| The beam exists in a vacuum. | The current exists in a conducting material. |
| The electrons accelerate in a constant in-line electric field. | The electrons move at constant average velocity in a constant in-line electric field. (Resistance effect) |
| The beam is deflected by a constant perpendicular external electric field. | The conductor is not moved by a constant perpendicular external electric field. |
| Inter-beam interactions are just between electrons. | Inter-conductor interactions are between electrons and between electrons and protons. |
| Parallel beams, moving in the same direction, repel. | Parallel currents, moving in the same direction, cause the conductors to attract. |
| Parallel beams, moving in opposite directions, repel more. | Parallel currents, moving in opposite directions, cause the conductors to repel. |
These differences in behaviour are easily explained by the principle of a force induced by relative acceleration as in the motor effect'.
The force between passing charges
Consider two charges A and B. B
passes A, in a vacuum, as in the scenario described in the 'Preface to
the motor effect' topic. Using the same terminology as in the 'Motor
effect' topic, let the additional force between them
at closest approach, due to their relative motion,
be k.v2/d.
The
value of k
Besides v2/d, the force on the charges
depends on several factors which are bound up in k.
- The charge of A. (Call it q1)
- The charge of B. (Call it q2)
- The electrical property of the
intervening vacuum. (Call it Pe)
- The inverse of the square of the distance between the charges. (Call it 1/d2) - Point or spherical bodies.
Combining
the above factors into k:
k
= Pe.q1.q2/d2
The
additional force between the charges:
f = k.v2/d
f =
Pe.(v2/d).q1.q2/d2
f = Pe.q1.q2.v2/d3
From the 'Motor effect' topic:
Ka
= Pe/d
f = Ka.q1.q2.v2/d2
But:
Ka
= Ke/c2
So:
f = Ke.q1.q2.v2/c2.d2
The
additional force between the charges:
f = Pe.q1.q2.v2/d3
= Ka.q1.q2.v2/d2 = Ke.q1.q2.v2/c2.d2
The general equation is:
f = Ke.q1.q2.v2.(sin2θ)/c2.d2 (θ is defined in 'Preface to the motor effect'')
The force between static charges
Consider
two charges A and B, each value q, distance d apart in a vacuum. Using
the same terminology as in 'The force between passing charges' topic,
let the force between them be k.v2/d.
I will explain the significance of v later.
The
value of k
Besides v2/d, the force on the charges
depends on several factors which are bound up in k.
- The charge of A. (Call it q1)
- The charge of B. (Call it q2)
- The electrical property of the
intervening vacuum. (Call it Pe)
- The inverse of the square of the distance between the charges. (Call it 1/d2) - Point or spherical bodies.
Combining
the above factors into k:
k
= Pe.q1.q2/d2
The
force between the charges:
f = k.v2/d
f =
Pe.(v2/d).q1.q2/d2
f = Pe.q1.q2.v2/d3
Compatibility
with conventional terminology
In conventional terminology the force between two different static
charges in a vacuum is expressed as:
f =
(1/4π.ε0).q1.q2/d2 or
f = Ke.q1.q2/d2
So the electric force constant Ke = Pe.v2/d.
What is the meaning of v in this context?
Ke = Pe.v2/d
From the 'Motor effect' topic:
Ka = Pe/d
So:
Ke/Ka = v2
However, Ke/Ka = c2 where c is the speed of light in a vacuum.
So:
v = c
The force between the charges:
f = Pe.q1.q2.c2/d3 = Ka.q1.q2.c2/d2
=
Ke.q1.q2/d2
So the force between two static charges, distance d apart, is equal to the additional force that would be induced between one stationary charge, and the other passing with velocity c at distance d.
I will deal with the issue of the mass associated with a charged particle in another topic.Electrons and magnets
To avoid discussion as to the cause of ferro-magnetism, and for the sake of simplicity, all the magnets described below are simply coils consisting of one turn, radius d, of a current-carrying conductor.Why magnetic poles attract or repel
Two coils on the same axis with the electron flows in the same direction attract due the motor effect as described previously.
Similarly, two coils on the same axis with the electron flows in opposite directions repel due the motor effect.
The motion of an electron, in a vacuum, passing across a pole of a magnet
The forces described here are in addition to other electrical forces on the particles.
There is a lone electron ea, in a vacuum, passing across a pole of a magnet.
- For simplicity, all the moving particles move with velocity v with respect to the coil.
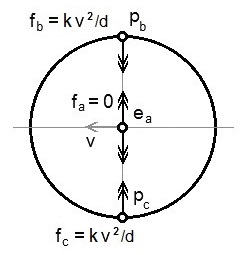 |
Using the same argument with other pairs of protons you can show that there is no net force on the lone electron due to all the protons in the conductor.
Now consider the interaction of the lone electron ea with two free electrons, eb and ec moving in the conductor either side of the path of ea. The scenario is similar to the motor effect. Electron eb is moving in the same direction and at the same speed as ea, so there is no additional force. Electron ec is moving past in the opposite direction to ea, so there is an additional repulsive force between them.
 |
Using the same argument with other pairs of electrons you can show that there is a net force on the lone electron, acting at right angles to its direction of travel, due to all the free electrons in the conductor. The pair either side of the lone electron result in the maximum force. The pair directly ahead and behind the lone electron result in the minimum force, a quarter of the maximum.
The result of this sideways force is that the lone electron is deflected and tends to move in a circular path in the opposite sense to the flow of electrons in the coil.
There is also an axial, repulsive, component of the force. This is why electrons 'spiral' (helical-spiral) away from a pole of a magnet.
If the lone electron passes between two identical coils, parallel to the planes of the coils, these axial components cancel and the lone electron moves in a circular path parallel to the planes of the coils. The motion of an electron experiencing a force is limited by the interaction between its mass and the universal gravitational presence. In 1897, J J Thompson used this scenario to determine the ratio e/m (I would call it qe/me), the ratio of charge to mass for an electron.
Inertial frame dragging
Inertial frame dragging is gravitational equivalent of the last topic.Einstein's general theory of relativity predicts that non-static, stationary mass–energy distributions affect spacetime in a peculiar way giving rise to a phenomenon usually known as frame-dragging. The first frame-dragging effect was derived in 1918, in the framework of general relativity, by the Austrian physicistsJosef Lense and Hans Thirring, and is also known as the Lense-Thirring effect. They predicted that the rotation of a massive object would distort the spacetime metric, making the orbit of a nearby test particle precess. - from Wikipedia.
This is my understanding of inertial frame dragging:
- A satellite is in a polar orbit round a planet. It experiences a sideways force due to the rotating planet below it. This force causes the orbit to precess in the same sense as the rotation of the planet.
I would like now to try to explain inertial frame dragging in terms of the principle of a force induced by relative acceleration. This is not intended to compete with General Relativity, but to offer another way of looking at the phenomenon.
- For simplicity, let the planet be represented by a thin rotating massive torus, and the satellite by a massive object ma passing over the axis of the torus.
-
Let the velocity of the object, v, be equal to the tangential velocity of the torus. The radius of the torus is d.
- The forces described here are in addition to other gravitational forces on the bodies.
 |
Using the same argument with other pairs of masses you can show that there is a net force on the object, acting at right angles to its direction of travel, due to all the mass in the torus .
The result of this sideways force is that the object is deflected and tends to move in a circular path in the same sense as the rotation of the torus. This is in addition to the motion due to the gravitational attraction perpendicular to the plane of the torus.
There is also an axial attractive component
of the force.
In the case of a satellite in a polar orbit round a planet, the deflecting force causes the orbit of the satellite to precess in the same sense as the rotation of the planet.
The frame dragging effect operates to some extent on all orbits except the synchronous equatorial orbit.
It seems that Inertial Frame Dragging is due to a gravitational effect, equivalent to magnetism. Another phenomenon in this category is Perihelion Precession.Perihelion Precession
If a body orbits the sun in an eliptical orbit the point of closest approach is the perihelion. The point of greatest separation is the aphelion. It was observed that the position of the perihelion of the planet Mercury is not fixed but gradually moves around the sun with respect to the fixed stars. This phenomenon is called Perihelion Precession. (The position of the aphelion does the same).The suffix 'helion' refers to the sun (Greek - helios). The equivalent terms to perihelion and aphelion, for any two bodies in orbit around one another, are periapsis and apoapsis. The suffix 'apsis' refers to the points where an ellipse intersects its major axis.
Two massive bodies moving past one another will experience an attractive force in addition to the static gravitational force. This is the gravitational equivalent of the Motor Effect, described previously.
If two massive bodies are in orbit around one another, and the orbits are elliptical, the orbital speed is greatest at periapsis. At this time their relative acceleration is at a maximum away from one another. This results in an attractive force on the bodies, in addition to the static gravitational force, causing the orbits to 'contract' near periapsis.
The orbital speed is lowest at apoapsis. At this time their relative acceleration is at a maximum towards one another. This results in a repulsive force on the bodies, in opposition to the static gravitational force, causing the orbits to 'expand' near apoapsis.
These effects are additive and combine to cause the orbits to be distorted so that the orbital axes precess in the same sense as the orbital movement of the bodies. These effects are not present if the orbits are circular as the distance between the bodies is constant.
Other terms
for Perihelion Precession are Periapsis Precession, Apsidal Precession
and Orbital Precession.
The force between passing masses
Consider two masses A and B. B
passes A, in a vacuum, as in the scenario described in the 'Preface to
the motor effect' topic.
Using similar terminology to
the 'The force between passing charges' topic. Let the additional force
between them due to their relative motion
at closest approach
be k.v2/d.
The
value of k
Besides v2/d, the force on the masses
depends on several factors which are bound up in k.
- The mass of A. (Call it m1)
- The mass of B. (Call it m2)
- The gravitational property of
the intervening vacuum. (Call it
Pg)
- The inverse of the square of the distance between the masses. (Call it 1/d2) - Point or spherical bodies.
Combining
the above factors into k:
k
= Pg.m1.m2/d2
The
additional force between the masses:
f = k.v2/d
f =
Pg.(v2/d).m1.m2/d2
f = Pg.m1.m2.v2/d3
In a similar way to charge, let there be a constant associated with
moving masses, called Km.
Km = Pg/d
So:
f = Km.m1.m2.v2/d2
In the following topic I make the assumption that the gravitational constant G = Kg = Km.c2.
In which case:
f = Kg.m1.m2.v2/c2 d2
The additional force between the masses:
f = Pg.m1.m2.v2/d3 = Km.m1.m2.v2/d2 = Kg.m1.m2.v2/c2.d2 = G.m1.m2.v2/c2.d2
This equation applies when the masses are at closest approach.
The general equation is:
f = Kg.m1.m2.v2.(sin2θ)/c2.d2 (θ is defined in 'Preface to the motor effect')
The
force between static masses
Consider two masses A and B,
distance d apart, in a vacuum.
Using the same terminology as
in 'The force between static charges' topic, let the force between them
be kv2/d.
I will explain the significance of v later.
The
value of k
Besides v2/d, the force on the masses
depends on several factors which are bound up in k.
- The mass of A. (Call it m1)
- The mass of B. (Call it m2)
- The gravitational property of
the intervening vacuum. (Call it
Pg)
- The inverse of the square of the distance between the masses. (Call it 1/d2) - Point or spherical bodies.
Combining
the above factors into k:
k
= Pg.m1.m2/d2
The
force between the masses:
f = k.v2/d
f =
Pg.(v2/d).m1.m2/d2
f = Pg.m1.m2.v2/d3
Compatibility with conventional terminology
In conventional terminology the force between two different static masses in a vacuum is expressed as:
f = G.m1.m2/d2
Where
G is the gravitational constant. For consistency let G be known as Kg.
So the gravitational constant, G = Kg = Pg.v2/d.
What is the meaning of v in this context?Kg = Pg.v2/d
From the 'The force between passing masses' topic:
Km = Pg/d
So:
Kg/Km = v2
However, when dealing with charge, Ke/Ka = c2 where c is the speed of light in a vacuum.
For now, assume that:
v = c
The force between the masses:
If the above assumption is correct, the force between two static masses, distance d apart, is equal to the additional force that would be induced between one stationary mass, and the other passing with velocity c at distance d.
Inertia
A massive object, m, is accelerated with respect to the Universal Gravitational Presence.
Let the acceleration be a, the mass of the object be m, the mass of the visible Universe be M, and the extent of the Visible Universe from the object, the 'proper' (corrected for expansion) radius, be R.
The mass of the visible
Universe can be represented by a
mass M spread evenly over a spherical
surface, radius D, centred on m, where D is the mean distance of M from
m.
Presence can be considered to
have two properties, magnitude and acceleration. At distance d from a
massive body, m', the magnitude is proportional m'/d2
in the direction of m'. At the centre of the massive spherical surface
described above, the magnitude will be proportional to
M/D2. However the acceleration components cancel out and
there is no attraction towards any part of the surface. (This
is the gravitational equivalent of the absence of an electric field
inside a charged hollow sphere)
The force needed to accelerate
m is proportional to a, (f = k.a).
The value of k
Besides a, the force needed to accelerate the
object depends on several factors
which are bound up in k.
- The mass of the object. (m)
- The mass of the visible Universe. (M)
- The gravitational property of the intervening space. (Call it Pg)
- The inverse of the square of the distance of M from
the object. (1/D2).
Combining
the above factors into k:
k
=
Pg.M.m/D2
Assuming,
as in the previous topic:
G = Kg
=
Pg.c2/D
(Kg is
the gravitational constant)
Pg
= Kg.(D/c2)
So:
k = Kg.(D/c2).M.m/D2
k = Kg.M.m/c2.D
Estimating the mass of the Visible Universe, M
If
f = k.a and f = m.a:
k = m
m = Kg.M.m/c2.D
Kg.M/c2.D
= 1
M = D.c2/Kg
So:
M = R.c2/2Kg
- The 'proper' radius of the visible Universe,
R, is currently estimated at 4.4 x 1026
m.
- The square of the speed of
light, c2, is 8.9876 x 1016 m2 s-2.
- The gravitational
constant, Kg, is 6.67384 x 10-11 m3 kg-1 s-2.
M = 2.963 x 1053 kg
It is generally assumed that the terms M, Kg and c are constants over time. However there is no direct evidence for this. I wonder if R were to be a constant whether a combination of the other terms could explain the observations such as the Big Bang, expansion and so on, which would then be an illusion.
Preferred
terms and expressions
Electrical
effects
If
all electrical effects can be explained by charge alone then many
conventional terms become redundant. These include Ka,
μ0, B, H and even ε0. This makes electrical theory much easier to
understand.
My preferred constants are Ke and c. Pe is not a constant. (Pe = Ke.d/c2)
The motor
effect:
f = 2Ke.i1.i2.l/c2.d
Static charges:
f = Ke.q1.q2/d2
Passing charges: f = Ke.q1.q2.v2.(sin2θ)/c2.d2 (Additional force due to relative motion)
Gravitational
effects
My preferred constants are Kg
(= G) and c. Pg
is not a constant. (Pg
= Kg.d/c2)
Static masses:
f =
Kg.m1.m2/d2
Passing
masses:
f = Kg.m1.m2.v2.(sin2θ)/c2.d2
(Additional force due to relative motion)
Other
considerations
The
effect of universal presenceAny massive object, changing velocity, is subject to universal presence which tends to oppose such a change. The magnitude of a gravitational interaction such as Inertial Frame Dragging is tiny. On the other hand, the magnitudes of equivalent electrical interactions are considerable and easily measured.
Conjecture 7
- The existence of universal gravitational presence and the absence of universal electrical presence are the reasons why gravitational effects are very much weaker than equivalent electrical effects.
In the Inertial Frame Dragging topic I said, "The frame dragging effect operates to some extent on all orbits except the synchronous equatorial orbit."
If a disc object is knocked axially out of its orbit, by a collision for instance, the forces I describe in the inertial frame dragging topic will tend to guide it back to a stable orbit in the disc.
Could this be the explanation of the stability of the ring system of Saturn, the fact that an accretion disc formed around the young sun and account for the disc shape of spiral galaxies?
In the outer reaches of the
solar system, in the region of the Kuiper Belt
and beyond, objects can have orbits more and more inclined to the Sun's
equatorial plane the
further out they are. This is because, at these distances, the effect
of the
rotating sun is so small that the orbits of objects originating in the
cloud of gas and dust, from which the Solar System formed, have not yet
had
time to be 'dragged' into the Sun's equatorial plane.
Remember Conjecture 6?
- On a cosmic scale and to a first approximation charge exhibits radiation but no presence, and mass exhibits presence but no radiation.
A. Because the speed of light is finite.
Two equal orbiting massive bodies are viewed from a point on the plane of their circular orbit. When they are seen side-by-side, the one on the left is accelerating to the right and the one on the right is accelerating to the left. Because the effects of their motions travel at a finite speed, the approaching mass appears to move faster than the receding mass. Acceleration in a circular orbit varies with the square of the velocity. From the point of view of the observer there is a net transverse acceleration at this time.
When they appear in-line with the observer, one is behind the other. Because the effects of their motions travel at a finite speed, the furthest one appears retarded in its orbit and the nearest one more advanced. From the point of view of the observer there is also a net transverse acceleration at this time, but in the opposite direction to the side-by-side situation. In between these times there are transverse and in-line components to the observed net acceleration.
The observed changes in acceleration are experienced as gravitational radiation by the observer. The frequency of the radiation is twice the frequency of the orbital rotation.For a fuller explanation of this scenario, see the Appendix at the end of my Gravitational radiation article.
A consequence
for the the inverse square force law
All
the phenomena discussed in this article, gravitational and electrical,
can be explained by the concept of a force induced by realtive
acceleration.
An
interesting outcome
is that the inverse square force law only applies when bodies are at
rest relative to one another. The inverse square force law has to be
modified if there is a relative acceleration between them, as in the
case of rotating, orbiting or passing bodies.
Much more speculative scenarios
These are the subject of other articles.| Negative mass | Why masses attract |
Mike Holden - Feb 2013 to Sep 2017